Фу, жарко!... Работу я кончил давно,
Не хочется больше трудиться.
И спать не хочу ... Отворяю окно,
Чтоб свежестью ночи упиться.
Вон вижу я — темный и мрачный завод
Стоит у огромного пруда.
Как много он в жизни работы дает
Для бедного, черного люда!
Питает и кормит он этих людей,
Но как непригляден и страшен
Он в светлой ночи темнотою своей,
Лишь дымом да мраком украшен! (27 января 1899)

Б. Н.Орлов (18721911)

Ключевые понятия

Производство Предельная норма технического замещения

Ресурсы (факторы производства) Средний продукт

Производственная функция Предельный продукт

Фирма Производительность труда

Претендент на доход Производительность капитала

Чистая (экономическая) прибыль Три стадии производства

Нормальная прибыль Эластичность замены

Краткосрочный период производства Изокоста

Долгосрочный период производства Изоклиналь

Изокванта Отдача от масштаба

Интенсивное производство «Пограничная линия»

Экстенсивное производство Эластичность выпуска

Предыдущая (четвертая) глава была посвящена исследованию природы кривой спроса. В ней было выяснено, какой объем благ будут приобретать экономические агенты при условии, если они действуют «рационально». При этом под рациональ­ ным поведением потребителей понималось сопоставление выгод (полезности) потреб­ ления различных объемов благ или комбинаций этих благ с затратами (ценами).

Теперь (в главах пятой и шестой) нам необходимо исследовать природу кри­вой предложения и выяснить поведение рационального производителя (или фир­мы). При этом мы должны исследовать выгоды и затраты фирмы, производящей различные объемы благ и применяющей различные методы производства. Мы должны выяснить:

• какой объем продукции должна производить фирма;
• какая комбинация факторов производства при этом должна применяться;
• сколько прибыли будет получено в результате производства.

Производством является любая человеческая деятельность , в процессе которой ресурсы превращаются в товары и услуги .

Производство наряду с распределением, обменом и потреблением является од­ним из четырех основных видов активности, которые обеспечивают экономиче­ское благополучие общества. Производственная активность существенно видо­изменяется в процессе развития общества. Потребление может существовать и без производства. Тем не менее в реальной действительности эти два вида чело­веческой деятельности неотделимы друг от друга, так как ресурсы крайне редко могут потребляться без предварительной обработки.

Производство не обязательно должно происходить на «заводе» или «фабрике». Домашние хозяйства также осуществляют определенную деятельность, превращая рыночные блага в продукт потребления. Приготовление пищи, стирка, чистка — все это является производственной активностью, которая трансформирует рыночные блага в конечные продукты потребления; время индивида также является производ­ственным ресурсом с множеством альтернативных возможностей использования.

Основные ресурсы ( inputs ), такие как земля, труд, капитал, принято именовать факторами производства. Зависимость между ресурсом и конечным продуктом называется производственной функцией и является важнейшей категорией про­изводства.

Производственная функция : физическое отношение между произведенным объ­емом выпуска ( output ) и количеством используемого фактора производства ( input ) при предположении технической эффективности .

Так как производственные решения, как правило, принимаются отдельными фирмами, то прежде всего необходимо рассмотреть природу фирмы, особенности ее деятельности, а также основные законы производства.

Ктото мрачный, как в видике «Шокер», К нам подкрался и, выждав момент, Прошептал мне с улыбкой: «Я брокер... Скоро сделаю вам менеджмент...»
А. В. Бардодым (19661992)

Домашнее хозяйство и фирма являются главными действующими лицами рыночных отношений.

Фирма 1 — это организация , созданная для производства товаров и услуг с целью их продажи на рынке .

• 1 Происхождение слова «фирма», прочно вошедшее во многие языки мира, восходит к латыни: firmus прочный, надежный, (юридически) действительный. Значению «фирма» в какойто мере соответствует русское слово «предприятие». Фирма (предприятие) мо­ жет состоять из одного или нескольких заводов, фабрик и учреждений.

Фирма приобретает ресурсы, организует их потребление в процессе производ­ства, реализует произведенную продукцию и участвует в процессе принятия рис­ ков. Индивиды, участвующие в деятельности фирмы, состоят из предпринимателей и рабочей силы. Главное различие между ними заключается в том, что предпринима­тели являются претендентами на доход ( residual claimants ), т. е. обладают претензи­ ей или правами собственности на прибыль, полученную организацией.

Претендент на доход ( residual claimant ): индивид , который обладает законными правами на всю или часть прибыли , получаемую фирмой .

Что касается рабочей силы, то она получает фиксированную заработную плату независимо от объема прибыли фирмы. И хотя подобное различие предпринима­ телей и рабочей силы порой более или менее успешно маскируется различными типами заработной платы (такими, например, как «участие рабочих в прибы­ лях»), тем не менее оно остается существенным.

Одна из основных причин существования фирмы заключается в том, что ко­ операция между отдельными работниками способна давать больше продукции при данном объеме ресурсов. Производство более эффективно, если индивиды специализируются на выполнении конкретных производственных задач. Вмес­ те с тем кооперация невозможна без организации и менеджмента: (1) рабочие должны знать, что им следует делать, и (2) должны выполнять на деле то, что им следует.

Так как рабочая сила не является претендентом на доход, то у нее отсутствуют реальные стимулы к выполнению и к совершенствованию производственного процесса. Поэтому деятельность рабочей силы требует управления и надзора либо со стороны предпринимателей, либо со стороны других наемных работни­ ков (менеджеров или надсмотрщиков). Пока доходы от более эффективного про­изводства фирмы превышают расходы, а кооперативное производство выпускает больше чистого продукта, чем множество индивидуальных предприятий, — до тех пор организация типа «фирма» способна существовать и развиваться.

Производственный менеджмент также является важным фактором производ­ ства: без него объем производства существенно снизится. Несение коммерческого риска также является фактором производства и осуществляется предпринимате­ лем. Таким образом, предприниматель, или владелец предприятия, обычно являет­ся не только претендентом на доход, но и активным участником производственно­ го процесса.

Бизнесмен может быть собственником, организатором, менеджером и пред­ принимателем риска в одном лице. Его доход, извлекаемый из деятельности фир­ мы, состоит из двух частей: претензии на доход (известной как чистая, или эконо­ мическая, прибыль или сверхприбыль) и полного жалованья по оплате его усилий (известного как нормальная прибыль).

Чистая ( экономическая ) прибыль ( л ) — общий доход фирмы ( Pq ) за вычетом вме­ненных издержек ( С ).

Нормальная ( или нулевая экономическая ) прибыль — часть предприниматель­ского дохода ( минимальный доход , которым должны вознаграждаться предприни­мательские способности , чтобы стимулировать их применение в предпринимательской деятельности фирмы ), вмененные издержки . Если фирма получает толь­ко нормальную прибыль , то ее доход полностью расходуется на покрытие всех из­держек .

Математически величину чистой (экономической) прибыли фирмы можно выразить так:

n = Pq C ( q ), (5.1)

а нормальной (или нулевой экономической) прибыли:

я 0 или Pq = C ( q ). (5.2)

Однако собственник может быть представлен большим количеством акционе­ ров, каждый из которых имеет часть претензии на прибыль, несет долю риска и не принимает непосредственного участия в производственном процессе.

При всей важности данных рассуждений наш анализ может быть в значитель­ ной степени упрощен, если мы сосредоточимся на рассмотрении двух наиболее осязаемых факторов производства (труд и капитал), оставив в стороне менее явные: «предпринимательские способности», «несение риска», «организацион­ ный талант». Менее очевидные факторы производства обыкновенно рассматри­ ваются в рамках специальных экономических дисциплин, таких как «теория фир­ мы», «теория предпринимательства», «менеджмент».

В курсе микроэкономики роль собственника сводится к покупке ресурсов и их комбинированию в процесс производства с целью максимизации прибыли. Ибо именно это составляет основу микроэкономической модели фирмы.

Микроэкономическая теория основывается на предположении , что фирма стремит­ся к максимизации долгосрочной прибыли .

Вместе с тем существует множество альтернативных теорий, отрицающих, что максимизация прибыли — главное в деятельности фирмы. Как правило, подоб­ ные теории исходят из следующих предположений:

• разделение функций собственности и контроля фирмы;
• подробное рассмотрение предпочтений предпринимателя.

Разделение функций собственности и контроля предполагает, что собственни­ ки нанимают менеджеров для принятия решений и что менеджеры не являются пре­ тендентами на доход. Поэтому менеджеры стремятся не столько к максимизации прибыли фирмы, сколько преследуют собственные интересы. Стремления менед­ жеров могут включать высокое жалование или такие удовольствия, как раздутый управленческий штат, роскошные апартаменты и разнообразные льготы. Ряд наи­более известных теорий фирмы ставят в центр внимания зависимость управленче­ских окладов от общего объема продаж (за вычетом издержек) и темпов роста.

• 1 Именно долгосрочная перспектива получения прибыли определяет рыночную сто­ имость предприятия. Если предприятие заинтересовано лишь в текущей (краткосрочной) прибыли, то оно способно увеличивать ее методами, которые сокращают будущую доход­ ность (отказ от надлежащего ухода за оборудованием, игнорирование научнотехническо­ го прогресса и т. п.).

Концепция предпочтений предпринимателя исходит из того, что менеджеры преследуют цели не выше тех, которые бы доставили удовлетворение владельцу фирмы (другими словами: если собственник доволен, к чему менеджеру продол­жать оптимизировать производство?).

Существуют и другие теории, которые рассматривают предпринимателей как особых индивидов, обладающих уникальными предпочтениями: стремлением к новациям, коммерческому риску и т. п.

Прочие менее значительные факторы производства (издержки мониторинга или организации, принятие рисков и т. д.) также подробно анализируются некоторыми теориями фирмы. Однако они не отрицают ведущей концепции максимизации прибыли, а скорее являются ее уточнением и конкретизацией.

В курсе микроэкономики основное внимание уделяется частным коммерче­ским предприятиям, управляемым в интересах собственников и максимизирую­щим долгосрочную прибыль, как наиболее распространенному и типичному виду фирмы в условиях рыночной экономики.

Пробил час и пора настала
для брачных уз Труда и Капитала.
Блеск презираемого металла
(дальше — изображение в лицах)
приятней, чем пустота в карманах,
проще, чем чехарда тиранов,
лучше цивилизации наркоманов,
общества, выросшего на шприцах. (14 января 1967)

И. Бродский (19401995)

Экономический анализ производства исследует отношение между затрата­ми ( input ) и выпуском ( output ). Это отношение, известное как производственная функция, определяет максимальный объем выпуска при определенных комбина­циях факторов производства. Производственная функция исходит из трех основ­ных упрощений.

Вопервых, поскольку производственная функция имеет дело с максимумом выпуска,.соответствующего различным комбинациям факторов производства, постольку использование производственной функции подразумевает, что про­цесс производства является технически эффективным. Буквальная интерпрета­ция этого допущения сводится к тому, что возможность ошибок и потерь полно­стью исключена. Однако контроль ошибок и потерь является важной функцией менеджмента. Поэтому рассмотрение обычной производственной функции под­разумевает игнорирование менеджмента.

Вовторых, временные рамки анализа должны быть достаточно короткими, так чтобы технология (технический прогресс) рассматривалась в качестве посто­янной величины, не влияющей на факторы производства (труд и капитал).

Втретьих, предполагается, что ресурсы способны замещать друг друга. Это означает, что данный объем производства (выпуска) может быть получен на основе различных комбинаций факторов производства.

В самой общей форме производственная функция для п факторов производ­ ства может быть записана следующим образом:

Q Q (/ 1( .../„), (5.3)

где Q — объем выпуска фирмы за определенный период времени;

/ — объем затрат факторов производства за определенный период времени. Обычно в стандартных курсах макроэкономики рассматривают двухфакторную производственную функцию типа:

Q = Q ( L , K ), (5.4)

где L и К — объемы применяемого труда и капитала.

Ограничение производственной модели двумя переменными является созна­ тельным упрощением действительности. Каждая единица затрат предполагается величиной гомогенной (однородной). При этом подразумевается, что в производ­ ственной функции типа Q = Q ( L , К) час труда идентичен любому другому часу труда. К примеру, один рабочий в течение двух часов создает тот же объем выпус­ ка, что и двое рабочих в течение одного часа. Каждая единица капитала также предполагается одинаково продуктивной.

На стенках тихо виснут мухи, Он забывает про кручину,
Которые от скуки мрут, Он забывает про беду...
И Сидоров — из ремеслухи — Сто тысяч шайб — готова смена,
Берется за серьезный труд. Но не утрачен интерес,
Он, словно бог, стоит у пресса И вновь с упорством супермена
И нажимает на педаль, Жмет Сидоров, грохочет пресс.
Деталь из черного железа Чернейший, словно африканец,
Кругла, как с дыркою медаль! Чернее, чем фабричный чад.
Он жмет проклятую пружину — Жмет на педаль, не отвлекаясь,
И снова шайба на лету, Лишь зубы белые торчат... (1991)

С. М. Мнацкатян

Производственная функция основана на ряде «особенностей производства». Особенности производства касаются эффекта выпуска в трех основных случаях: (1) пропорциональное увеличение всех затрат; (2) изменение структуры затрат при постоянном выпуске; (3) увеличение одного фактора производства при ос­ тальных неизменных.

Случай (3) относится к производству в краткосрочном периоде.

Краткосрочный период производства : самый продолжительный отрезок време­ни , в течение которого возможно изменить объем применения лишь одного ресурса ( фактора производства ).

Фактор, количество которого может быть изменено в данный период времени, называется переменным. Напротив, фактор производства, количество которого нельзя изменить в пределах данного периода времени, за исключением случаев, предполагающих непомерно высокие затраты, называют постоянным по отноше­нию к этому периоду времени.

Случаи (1) и (2) относятся к долгосрочному периоду, когда все затраты изменя­ются.

Долгосрочный период производства : период времени , достаточный для того , чтобы все имеющиеся ресурсы фирмы могли стать переменными .

Особенности производства схожи с особенностями потребления (рассматри­ваемыми в главе 4) при одном существенном различии: если категорию «полез­ность» затруднительно измерить количественно, то отношения факторов произ­водства вполне измеряемы в натуральных единицах.

5.3.1. Объем выпуска при разных производственных процессах

На всех себя не хватит Чего они хотят? Чего хочу я? На себя Не хва! На всех.
Мирон Бялошевский (19221983)

Производственный процесс может быть определен как специфическая про­порция комбинации затрат для обеспечения определенного объема выпуска. Например, час труда одного рабочего и одной машины сформирует производствен­ный процесс двухфакторной модели трудкапитал. Два рабочих и одна машина — другой производственный процесс и т. д.

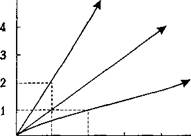
Предположим, что фирма может выбирать из трех производственных процес­сов, в которых отношения между капиталом (К) и трудом ( L ) находятся в про­порциях: 4:1; 1:1 и 1:4. Допустим также, что эти производственные процессы спо­собны давать объемы выпуска соответственно равные: 2, 1 и 2 ед., как это изображено в табл. 5.1 и на рис. 5.1.

Предполагается, что три рассматриваемые нами производственные функции имеют постоянную отдачу от масштаба. Постоянная отдача от масштаба озна­чает, что объем производства возрастает в прямой пропорции с увеличением факторов производства}

Отдача от масштаба ( returns to scale ) — отношение между темпами изменения вы­пуска и одинаковым для всех факторов темпом изменения объема их использова­ния .

• 1 На практике явление постоянной отдачи от масштаба маловероятно. Обычно по мере увеличения количества применяемого фактора производства на начальных стадиях выпуск возрастает ускоренно, а затем, достигнув некой величины, — замедленно (см. рис. 5.4), и, наконец, при преодолении определенного максимума объем выпуска начинает снижаться с дальнейшим увеличением переменного фактора производства. Далее (параграф 5.10) мы рассмотрим проблему переменной отдачи от масштаба подробнее.

Таблица 5.1
Параметры трех производственных процессов

Q

Вариант первый: Qi ( Kq , L ) = 21 (при K / L = 2 Vl )

Вариант второй: Q 2 1 (К 0 ,1) У 4 1 (при КД Vl )

Вариант третий: Оз = 2 (К 0 , L ) = У 2 1 (при А/1 = V 4 )

Рис . 5.1 . Производственная функция для краткосрочного периода с постоянной отдачей от масштаба { внимание : не путать с рис . 5.2, на котором по оси ординат — К )

Теперь рассмотрим, как изменяется объем выпуска при изменении перемен­ного фактора.

5.3.2. Объем выпуска при замене

Эх, машина миллионная, Дорогая электроника, кнопки красные, зеленые — Это вещь не для дальтоника. В ней идут процессы тайные, Непонятные движения — То сложенье—вычитание, То деление—сложение.

А когда уходят на ночь Все сотрудники с работы, Счетовод Степан Степаныч Достает из сейфа счеты. И, согласно указаниям, Он на счетах — дело тонкое Проверяет показания, Чудотехникою данные.
(1989) В. Е. Бохнов

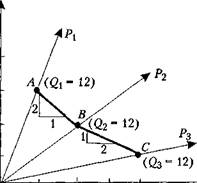
Производственная функция, учитывающая процесс изменения одного факто­ра на другой, изображена на рис. 5.2. Из начала координат проведены три луча. Первый луч иллюстрирует производственную функцию Q , = 21 (при K / L = 4/1). В данном случае при постоянной отдаче от масштаба комбинация 24 ед. капитала и 6 ед. труда дает 12 ед. выпуска (точка А).

Во втором производственном процессе (луч 2, производственная функция Q 2 = L , при K / L = 1/1)12 ед. каждого фактора производства также дадут 12 ед. выпуска (точка В).

В третьем производственном процессе (луч 3, производственная функция Q 3 = 1/2 L при K / L =1/4) комбинация 6 ед. капитала и 24 ед. труда также даст 12 ед. продукции (точка С).

Итак, точки А, В и С представляют одинаковые объемы выпуска ( Q , = Q 2 = Q 3 = = 12), но представляют собой разные производственные процессы. Соединяющая данные точки «кривая» ( ABC ), аналогичная кривой безразличия потребителя, получила название изоквантпы.'

О 6 12 18 24 L

Рис . 5.2. Процессы производства при разных сочетаниях ресурсов { внимание : не путать с рис . 5.1, на котором по оси ординат — О )

Изокванта ( линия равного выпуска — isoquant ) — кривая , представляющая множе­ство комбинаций факторов производства ( ресурсов ), обеспечивающих одинаковый выпуск продукции . 2

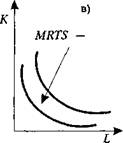
На отрезке АВ при замене одной единицы труда на две единицы капитала объем выпуска не изменяется. Таким образом, в данном случае предельная норма технического замещения ( MRTS ) труда на капитал равна двум.

Предельная норма технического замещения ( MRTS — marginal rate of technical substitution ): пропорция , в которой один фактор может быть заменен на другой при сохранении прежнего объема выпуска ; наклон кривой изокванты определяется ве­личиной MRTS .

Замена процесса производства 1 процессом 2 означает переход к более трудоинтенсивному процессу от более капиталоинтенсивного.

На отрезке между точками В и С процесс производства 2 заменяется процессом 3. В данном случае для замены одной машины требуются 2 ед. труда: предельная норма технического замещения ( MRTS ) труда на капитал уменьшилась (с 2 до 1/2). Таким образом, изокванты, как и кривые безразличия, выпуклы к началу координат. А это означает, что при движении вдоль кривой вправо величина MRTS уменьшае­тся. Принцип уменьшения MRTS связан с законом убывающей отдачи: каждая до­полнительная единица фактора производства приносит все меньшую отдачу.

• 1 Слово «изокванта» состоит из греческого компонента хаоС, («изос» — равный) и латинского quantitas — количество.
• 2 Изокванты для процесса производства означают то же, что и кривые безразличия для процесса потребления. Они обладают аналогичными свойствами: отрицательный наклон, выпуклость относительно начала координат, непрерывность и непересекаемость друг с другом.

MRTS LK =(5.6)

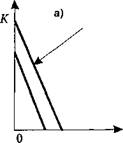
Изокванты, как и кривые безразличия, могут принимать разные формы. На рис. 5.3 изображены три вида изоквант:

• линейная с совершенной замещаемостью производственных ресурсов (рис. 5.3, а);
• с жесткой дополняемостью ресурсов, которую также называют изоквантой леонтьевского 1 типа (рис. 5.3, б);
• с непрерывной, но несовершенной замещаемостью (рис. 5.3, в).

5.3.3. Построение производственной функции с дискретным изменением переменного фактора

Вещи больше, чем их оценки.
Сейчас экономика просто в центре.
Объединяет нас вместо церкви,
Объясняет наши поступки.
В общем, каждая единица
По существу — девица.
Она желает объединиться.
Брюки просятся к юбке. (14 января 1967)

И. Бродский (19401995)

Построим график производственной функции с одним переменным факто­ром ( L ), который изменяется дискретно. Для этого вернемся к табл. 5.1.

Названа в честь лауреата Нобелевской премии В. В. Леонтьева (19061999).

Из табл. 5.1 следует, что в производственном процессе 1 каждая единица тру­ да ( L ) обеспечивает создание 2 ед. выпуска ( Q ); в производственном процессе 2 каждая единица труда обеспечивает создание 1 ед. выпуска; в производственном процессе 3 каждая единица труда обеспечивает создание 1/2 ед. выпуска.

Допустим, что количество применяемого капитала неизменно (формула = 24). Пусть производитель поначалу изберет производственный процесс 1, при кото­ ром используется наименьшее количества труда по отношению к капиталу, т. е. наименее трудоинтенсивный ( L / K ) или наиболее капиталоинтенсивный ( K / L ) процесс: формула = 24, L = 6.

Так как объем применяемого капитала неизменен и равен 24, объем выпуска ( Q ) в производственном процессе 1 не может превзойти 12 ед. (из условия табл. 5.1). На рис. 5.4 производственный процесс 1 изображен при помощи отрезка ОА.

Однако объем выпуска ( Q ) может быть постепенно увеличен с 12 до 24 ед. по мере замены производственного процесса 1 на производственный процесс 2.

Рассмотрим замену процесса 1 на процесс 2 на конкретном примере. Допу­ стим, что эта замена происходит при осуществлении предпринимателем 20 после­ довательных (дискретных) шагов.

А 'Стадия I !

2/i MP АР 2 |

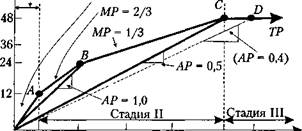
0 6 24 32 72 96 120 L

Рис . 5.4. Построение производственной функции с дискретным изменением L

Во время первого шага предприниматель продолжает использовать 22,8 (из 24) ед. капитала (или 95%) в производственном процессе 1, а 1,2 ед. капитала (или 5%) переводит в производственный процесс 2. В результате общий объем выпуска ( Q ) составит 12,6 ед. (11,4 ед. выпуска в производственном процессе 1 при участии 22,8 ед. капитала и 5,7 ед. труда +1,2 единицы выпуска при участии 1,2 ед. капита­ ла и 1,2 ед. труда).

Таким образом, при переводе 1,2 ед. капитала из производственного процес­ са 1 в производственный процесс 2 из производственного процесса 1 высвобо­ дилось 0,3 ед. рабочей силы, по в производственном процессе 2 понадобилось 1,2 ед. рабочей силы. Поэтому при частичном переходе с производственного процесса 1 на производственный процесс 2 объем выпуска увеличился на 12,6 12,0 = 0,6 ед. Занятость рабочей силы при этом увеличилась на 1,2 0,3 = 0,9 ед. и составила 6,9 ед.

Объем капитала остался неизменным (24 ед.). Но изменилась его структура: 22,8 ед. капитала задействованы в производственном процессе 1, а 1,2 ед. капитала — в производственном процессе 2. Ранее же весь капитал находился лишь в процессе 1.

При переходе от процесса 1 к процессу 2 объем производства увеличился на 0,6 ед. при увеличении занятости на 0,9 ед., т. е. предельная производительность труда при переходе к процессу 2 составила 2/3 ( MP L = AQ / & L = 0,6 / 0,9 = 2/3).

Во время второго шага предприниматель оставляет в производственном про­ цессе 1 только 21,6 ед. капитала (90%), разместив в производственном процессе 2 уже 2,4 ед. капитала (10%). Теперь общий объем выпуска составит 13,2 ед. (10,8 в процессе 1, плюс 2,4 в процессе 2). При этом общий объем использованного капи­ тала остался без изменения (формула = 24 ед.). Количество же рабочей силы сно­ ва возросло и составило 7,8 ед. (5,4 + 2,4).

И так далее (на протяжении 20 шагов), пока процесс 1 полностью не заме­ нится процессом 2 и объем выпуска ( Q ) не составит 24 ед. (достигнув точки В). При переходе от производственного процесса 1 к производственному процессу 2 предельная производительность труда (тангенс угла наклона отрезка 0В) со­ставляет 2/3.

При достижении выпуска объема Q = 24 ед. процесс 1 полностью прекращает­ся: теперь все производство осуществляется на основе процесса 2. С этого момен­ та дальнейшее увеличение выпуска возможно при переходе от производственно­ го процесса 2 к процессу 3, как это изображено на рис. 5.4.

При производстве первых 12 ед. выпуска, созданных в производственном процессе 1, каждая единица труда обеспечивает 2 ед. выпуска. Итак, в произ­ водственном процессе 1 и средний, и предельный продукты труда равны 2 ед. (АР = MP = 2), что изображено с помощью тангенса угла наклона отрезка 0А на рис. 5.4.

Средний продукт ( АР ), или производительность фактора , определяется как величина общего выпуска ( О ), поделенная на величину примененного фактора (/):

ap = q / i :

Предельный продукт ( MP ), или предельная производительность фактора , определяется как изменение выпуска ( ДО ), поделенное на соответствующее изме­нение фактора производства ( Ы ), при прочих постоянных величинах : МР = ДО / Д /. г

Таким образом, предельный продукт (или предельная производительность фак­ тора) равен:

• MPl = 4 T (предельная производительность труда); (5.7)
• МР К Т77 (предельная производительность капитала). (5.8)
• 1 Графически величина среднего продукта (АР) в данной точке равна тангенсу угла отрезка, соединяющего начало координат с данной точкой.
• 2 Графически величина предельного продукта ( MP ) в данной точке определяется как тангенс угла наклона касательной, проведенной к данной точке.

Средний продукт (или производительность фактора) равен:

• AP L = — (производительность труда 1 ). (5.9)
• АР К = — (производительность капитала). (5.10)

При увеличении выпуска с 12 до 24 ед. (точка В на рис. 5.4), т. е. при замене процесса 1 на процесс 2, величина MP L равна 2/3, a AP L = 1 (в точке В). Таким образом, на этом этапе MP L < AP L .

При производстве следующих 24 ед. выпуска до общей величины 48 (от точ­ ки В до точки С на рис. 5.4) происходит переход от процесса 2 к процессу 3 (т. е. на самую трудоинтенсивную технологию).

Таблица 5.2
Параметры производственной функции при дискретном изменении L

На данном этапе (от точки В к точке С) предельный продукт труда равен 1/3 (тангенс угла наклона отрезка ВС), а средний продукт, постепенно уменьшаясь (от 1), достигает величины S (тангенс угла наклона отрезка ОС) при объеме в 48 ед. (в точке С, когда используется лишь процесс 3).

Достигнув точки С, выпуск ( Q = 48) не может более возрастать бее увеличения объема уже имеющегося капитала. Предельная производительность труда дости­ гает нуля. Средняя производительность труда ( Q / L ) уменьшается, постепенно приближаясь к нулю при L —»°° . К примеру, 120 ед. труда дадут объем выпуска в 48 ед. при средней производительности труда, равной 48/120 = 0,4 (рис. 5.4). Ре­ зультаты этих расчетов обобщены в табл. 5.2.

Итак, на рис. 5.4 мы получили ломаную линию общего выпуска (ТР). Эта линия состоит из четырех отрезков, которые соответствуют: процессу 1 (отрезок 0Л); ком­ бинации процессов 1 и 2 (отрезок АВ); комбинации процессов 2 и 3 (отрезок ВС); а также процессу расточительной занятости труда (отрезок от точки С направо).

Обратим внимание на следующее.

На отрезке 0Л (стадия I ) неэффективно используется капитал («слишком много» капитала на данный объем производства), правее точки С (стадия III ) — неэффективно используется труд («слишком много» труда на данный объем про­ изводства). Поэтому рациональный производитель будет избегать работать на стадиях I и III . На рис. 5.2 этим районам соответствуют пространства, лежащие вне области PfiP y

• 1 Широко распространенный термин «производительность труда» есть не что иное, как средняя производительность фактора «труд».

Общая форма линии ТР отражает суть закона убывающей отдачи (предельной производительности), 1 который нами уже упоминался при рассмотрении MRTS .

Закон убывающей отдачи ( предельной производительности ): при увеличении одного фактора производства и неизменном другом достигается определенный объем выпуска , свыше которого величина предельного продукта начинает снижаться .

Необходимо особо подчеркнуть, что данный закон действует только в том случае, когда прочие факторы производства остаются неизменными. Если фиксированный до сих пор объем капитала будет увеличен, то кривая ТР сдвинется вправо и вверх.

5.3.4. Производственная функция с непрерывным изменением переменного фактора

Расчищая пред собой траекторию, проверьте
наличие нолей, лучей и стрелочек. Стрелки должны быть максимально подвижны
и закреплены на одной из книг. Ноли стабильны,
лучи устойчивы. Траектория прокладывается стрелочками, освещается лучами,
охраняемая знаками. (1998)
Е. Д. Марченко При бесконечном увеличении количества производственных процессов диск­ретная производственная функция превращается в непрерывную функцию. Напри­мер, данные табл. 5.3 соответствуют условию непрерывной функции Q = L i /2 K i /2 или частному виду производственной функции «КоббаДугласа». 2

• 1 Некоторые авторы утверждают, что это не закон, «а всего лишь общая черта, присущая большинству производственных процессов». См., например: Вэриан X . Р. Микроэкономика. Промежуточный уровень. М., 1997. С. 346.
• 2 Эта функция была использована в качестве одной из первых для статистической оценки производственного процесса. В самом общем виде она записывается следующим образом: Q = AL ° K \ где Л, а и Ь — параметры, определяемые статистически; причем а + b = 1.

Функции предельной производительности являются первыми частными производны­ ми относительно труда и капитала:

МР,=^ = аА& А) К ь ; МР К ^ = ЬАЕК^К
' 31 к дК

Если а и Ь положительны, предельный продукт также должен быть положителен, а зна­ чит, стадия III отсутствует. Если а<\ и Ь < 1, то предельные продукты труда и капитала убывают, что отражает уменьшение отдачи. Отметим, что частная производная от MP , от­носительно L имеет вид a ( a l ) AL °~ 2 К Ь и отрицательна при а < 1. Если а + Ъ = 1, то отдача от масштаба постоянна, так как удвоение К и L удваивает объем выпуска Q . Если а + b > 1, то отдача от масштаба возрастает. Величина среднего продукта имеет вид:

AP = < ^ = AW 4 b = I ^ L ; AP K =9 L ^ AL a K ^= Ml ] L .
1 L а к К b

Если 0 < a , b < 1, АР также снижается и MP < АР.

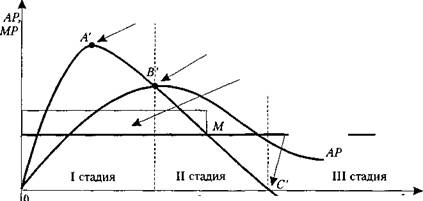
Параметры непрерывной (или классической) производственной функции изоб­ ретены в колонках 14 в табл. 5.3 и изображены графически на рис. 5.5. Предель­ный продукт (наклон кривой ТР) возрастает до точки В. Однако если до точки А рост идет возрастающими темпами (в точке А величина MP L = max ), то после точ­ ки А возрастание MP L происходит снижающимися темпами. В точке В на рис. 5.5 величина AP L = max . Это соответствует точке А на рис. 5.4.

Рис . 5.5. Производственная функция с непрерывным изменением L

Левее точки В на стадии I (рис. 5.5) часть капитала недоиспользована: здесь воз­ можно дополнительное привлечение переменного фактора ( L ) и соответствующее увеличение общего продукта (ТР). Поэтому фирма не станет планировать свой про­ изводственный процесс на стадии I . Оказавшись по какимто причинам на стадии I , предприниматель либо увеличит объем производства, наняв дополнительных рабо­ чих ( L ), либо попытается продать или сдать в аренду избыточные мощности (К).

Таблица 5.3
Параметры производственной функции при непрерывном изменении L

Рис. 5.6 иллюстрирует тот же самый процесс. Но здесь на оси ординат изобра­жено не Q , a MP и АР. Средний продукт (АР) достигает своего максимума в точке В' (соответствует точке В на рис. 5.5) и начинает уменьшаться. Предельный продукт ( MP ) достигает своего максимума в точке А' (точка А на рис. 5.5) и после этого также начинает уменьшаться. Таким образом, на стадии I величина MP больше ве­личины АР ( MP > АР).

Максимум MP

Максимум АР

Экономическая рента (квазирента)

Рис . 5.6. Кривые среднего и предельного продукта

По достижении границы стадии II (точка В') из условия ограниченного пред­ложения капитала следует, что дальнейшее увеличение объема выпуска может быть достигнуто лишь при переходе к более трудоинтенсивному процессу. Это значит, что и АР, и MP начнут уменьшаться. К тому же MP меньше, чем АР, так как более производительный процесс замещается менее производительным. На стадии II величина MP меньше величины АР ( MP < АР).

На границе между стадиями II и III (точки Си С), предельный продукт равен нулю ( MP = 0), а общий продукт (ТР) достигает своего максимума. Правее точки С каждая дополнительная единица труда приведет к сокращению объема выпуска. На стадии III величина MP < 0. Это значит, что рациональная фирма не будет участвовать в производственном процессе стадии III . Итак, рациональный эконо­мический выбор фирмы ограничен стадией II .

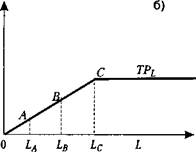
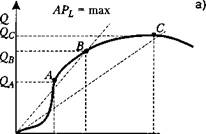
На рис. 5.7 приводится сопоставление взаимоотношений между общим, сред­ним и предельным продуктами производственных функций при непрерывном

• 1 Между MP и АР существует зависимость: MP = АР + L Формула зависимость ыводится следующим образом:

dAP L dL

эф

dL

L 2 ГдЬ

¦ Q ) = L ( MP L AP L ).

Это означает, что если MP L > АР Г то AP L возрастает. Если MP L < AP L , то AP L уменьша­ется. При максимуме AP L наклон AP L равен нулю, т. е. если dAP L / dL = 0, то AP L достигает своего максимума, если AP L = MP L .

(рис. 5.7, а) и дискретном (5.7, б) изменении переменного фактора L . При этом рис. 5.7, б упрощен по сравнению с рис. 5.4 (ломаная линия ОАВС изображена в виде прямого отрезка ОС).

APl MP,

MP L = AP L

MP L

Рис . 5.7. Сопоставление взаимоотношений между AP L и MP L при : а ) непрерывном и б ) дискретном изменении L

Специфика производственной функции при дискретном изменении перемен­ ного фактора сводится к тому, что на отрезке увеличения TP L (рис. 5.7, б) величи­ ны предельного и среднего продукта равны между собой. Это объясняется тем, что угол касательной к TP L и угол наклона самой линии TP L на ее восходящем участке совпадают между собой. Кроме того, при достижении TP L максимума и плавном уменьшении AP L линия предельной производительности труда ( MP L ) сливается с осью абсцисс, так как величина MP L равна нулю.

Существенной характеристикой технической результативности производства служит коэффициент эластичности выпуска по переменному фактору.

Коэффициент эластичности выпуска по переменному фактору ( e Q v ) показыва­ет , на сколько изменится выпуск при изменении объема переменного фактора ( v ) на одну единицу .

Запишем выражение коэффициента эластичности по переменному фактору следующим образом:

aQ / Q _ aQ у _МРу

E (2 v Av / v Av ' Q AP V ' ( 5Л1 >

Если мы рассмотрим изменение эластичности выпуска по труду на рис. 5.5, то на первой стадии производства величина г > 1, на второй стадии 1 > e UV ,> 0. На третьей стадии e & v , < 0.

И еще одна важная характеристика производственного процесса в коротком периоде. Речь идет об экстенсивном и интенсивном использовании фиксирован­ ного количества постоянного ресурса.

Экстенсивное производство 1 — производственный процесс , при котором объем выпуска происходит за счет прироста переменного фактора ( труда ).

Интенсивное производство 2 — производственный процесс , при котором главной причиной увеличения объема выпуска является повышение технического уровня производства .

Границы экстенсивного и интенсивного производства можно определить, если иметь в виду, что ^ = АР К = — (при К= 1, см. рис. 5.7, а). На стадии I и произво­ дительность труда ( AP L ), и производительность капитала (АР К ) возрастают. На стадии II производительность капитала продолжает возрастать, в то время как производительность труда падает. Поэтому стадия I есть стадия экстенсивного про­изводства: увеличение производства происходит здесь благодаря увеличению про­ изводительности обоих факторов. Стадия же II есть стадия интенсивного производ­ ства: увеличение производства здесь осуществляется лишь благодаря увеличению производительности капитала, а фактор труда себя исчерпал. Таким образом, гра­ница между стадиями I и II является границей экстенсивного производства, а гра­ница между стадиями II и III — границей интенсивного производства.

В пасмурное марево
В солнечное пекло
Снаряды полетели
Все до единого
Вовсе не туда куда им полагалось
Знать ошибочка прокралась в идеальные расчеты
Видно пушку заряжали нестерильными руками
Стало быть смешная вещь произошла. (1991)

Егор Летов

После того как мы выяснили, что рациональный предприниматель постарается ограничить объем выпуска стадией II (интенсивного производства), необходимо определить, какими именно параметрами определяется величина производства.

• 1 Extensivus (позднелат.) — расширительный, растяжимый.
• 2 Intensio (лат.) — напряжение, усилие.

Величина объема переменного фактора (труда), а значит, и объем производ­ства зависят от цены предельного продукта труда ( VMP L ). Фирма получит мак­симальную отдачу от имеющегося объема капитала в том случае, если количество применяемого труда соответствует условию: 1

PxMP L = VMP L = w , (5.12)

где Р — цена выпуска;

w — ставка заработной платы (цена труда).

Предположим, что Р = 4 р. (за единицу выпуска) и w = 8 р. (за единицу тру­да). Принимая во внимание особенности производства (табл. 5.3), фирма пред­почтет нанять 6 ед. труда, так как стоимость их предельного продукта равна 8 р. В среднем каждый работник произведет 2,5 ед. продукции ( AP L = 2,5) стоимос­тью 4 р. каждая. Таким образом, фирма получит излишек, или экономическую ренту ( R ), т. е. отдачу на свой фиксированный капитал:

R ( Px AP L w ) L = (4x2,5 8) х 6 =12.

Эта рента, или, как ее иногда называют, квазирента, 2 представляет собой отда­чу на фиксированный капитал. 3

Экономическая рента : это выплаты владельцу фактора производства сверх и по­мимо тех , которые необходимы для того , чтобы предотвратить перевод фактора в другую сферу его использования , т . е . платежи владельцу фактора , превышающие его альтернативную ценность .

Квазирента : это выплаты владельцу фактора , предложение которого в коротком периоде фиксированно . Если экономическая рента сохраняется как в длительном , так и краткосрочном периоде , то квазирента существует лишь в краткосрочном пе­риоде .

Таким образом, излишек достигает максимума при L * = 6. Данное решение проиллюстрировано на рис. 5.6. Величина L * соответствует пересечению линии MP L и горизонтальной прямой w / P . В данном случае линия MP L демонстрирует спрос фирмы на труд, а линия w / P — предложение труда при данной ставке зара­ботной платы. 4 Экономическая рента, представленная в единицах затрат, изобра­жена заштрихованным четырехугольником. Одна из его сторон равна разнице между AP L и w / P , вторая — величине L *.

• 1 Более подробно это условие будет рассмотрено в главе 11, посвященной анализу факторов производства.
• 2 Quasi (лат.) — как будто, словно, наподобие.
• 3 Строго говоря, термин «экономическая рента» относится к фактору, который фиксирован постоянно, а не только в краткосрочном периоде. Термин, который применяют к экономической ренте на капитал, в действительности является «квазирентой».
• * Более подробно об этом — в главе 11.

Я нервы наматывал на Бредовую сущность Командной системы. Но вскоре устал и взирая, На сломленный, сгорбленный дух, Не смел продолжать поединок. А надо бы. Надолбы. Лбы. (1991)

Хан Манувахов

Один из известных современных российских политиков Г. А. Явлинский поместил мо­ дель производственной функции в качестве теоретической основы своей версии о причинах краха советской плановой экономики. Приведем данную версию в кратком изложении. 1

Как пишет Г. А. Явлинский, в середине 1950х гг. в истории советской плановой эконо­ мики произошло знаменательное событие: именно тогда Политбюро впервые не смогло принять решения о пересмотре норм выработки для работников промышленности, транс­порта и связи, как это оно делало в предыдущие годы сталинского режима. Практически прекратился плановый пересмотр норм труда. Это было началом конца социализма. По­ чему это так?

В условиях СССР плановые органы выделяют государственным предприятиям ресур­ сы и ставят перед ними задачу максимального увеличения производства заданной про­дукции. Выпуск продукции есть функция от производительных затрат полученных ре­ сурсов.

Явлинский исходит из того, что плановая продукция сама по себе не интересует руко­ водство государственного предприятия и трудовой коллектив: если продукция произве­ дена в рамках плана, то ее необходимо всю без остатка сдать государству и никакая прода­ жа на свободном рынке невозможна. Чтобы реализовать продукцию на рынке, ее нужно какимто образом исключить из государственной плановой отчетности. То же самое каса­ ется и выделенных фондов — если какуюто часть из них удается реализовать «налево», то этот доход с черного рынка остается в распоряжении предприятия. Это основа суще­ ствования теневой экономики на уровне предприятий.

Если бы плановые органы могли до конца проконтролировать, как используются вы­ деленные фонды, возможности для теневой экономики не оставалось бы. Нечто подобное наблюдалось при Сталине. Впрочем, и тогда теневая деятельность не переводилась полно­ стью, но чем либеральнее становился режим, тем шире было для нее поле.

Если перевести все сказанное на экономический язык, то мы получим модель, где соб­ ственник (государство) делегирует производственные функции агенту (дирекции пред­ приятия), но не знает в точности его производственной технологии и не может проконтро­ лировать объем производительно затраченной части выделенных фондов. Собственник имеет лишь приближенное представление о том, какой объем продукции должен быть по­ лучен на выходе от предоставленного объема фондов (факторов производства). Это пред­ ставление он и доводит до агента (дирекции предприятия) в виде плана. Неисполнение плана влечет за собой штрафные санкции, которые превышают полезный эффект от теневой деятельности (лишение партбилета, арест). Перевыполнение плана тоже не имеет смысла: неучтенные лишние ресурсы и продукцию выгоднее продавать на черном рынке.

• 1 См.: Явлинский Г. А. Экономика России: наследство и возможности. Глава «Эволюция и крах советского планового хозяйства». М., 1995. С. 1631.

Таким образом, задача экономического агента, который знает свою производственную функцию, может быть сформулирована как максимизация ресурсов и готовой продукции, используемых в приносящей непосредственный доход теневой деятельности. Ограниче­нием при этом выступает необходимость выполнения государственного плана.

Явлинский исходит из того, что размер выделяемых предприятию фондов является предметом торговли между ним и государством, причем в определенных границах право выбора принадлежит предприятию. Точнее, государство не допустит, чтобы выделяе­мые фонды были ниже определенной или выше определенной верхней границы, но в этих границах выбирает предприятие. Оставляя в стороне нижнюю границу, мы увидим далее, что вопрос, выбирается ли полностью верхняя граница или нет, имеет принципи­альное значение.

Предположим, пишет Явлинский, что реальная производственная функция предпри­ятия имеет традиционную S образную форму (рис. 5.8). Это означает, что возрастающая отдача в начальный период деятельности предприятия (при низком уровне инвестиро­вания) затем сменяется убывающей отдачей по мере того, как нарастают сложности ко­ординации все более крупного производственного потенциала. Плановые же нормативы выпуска продукции задаются линейной функцией: требования к выпуску пропорцио­нальны объемам производственных фондов независимо от масштаба хозяйственной де­ятельности. Для того чтобы поставленная задача имела решение, необходимо, чтобы плановая прямая имела хотя бы одну общую точку с графиком производственной функ­ции (план был выполним хотя бы для одной комбинации фондов и выпуска готовой про­дукции).

А План, Производственная функция (7Р)

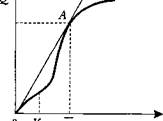
Q — объем выпуска готовой продукции;

К — фонды (капитал);

/ — инвестиции [(разница между объемом

капитала в текущем (К) и прошлом

( K t _ t ) периоде];

Kj нижняя граница фондов;

К — верхняя граница фондов.

Рис . 5.8. Плановая экономика в экстенсивной фазе ( сталинский плановый режим )

Далее Явлинский формулирует основные исходные положения своей модели.

Плановая экономика в экстенсивной фазе. Экономические агенты (директора пред­приятий) максимизируют полезность, извлекаемую из ресурсов, оставшихся на теневую деятельность (общий размер полученных фондов минус те ресурсы, которые израсходо­ваны на инвестиционную деятельность). Ограничением выступает плановая функция, которая растет пропорционально (в линейном отношении) размеру полученных ресурс­ных фондов. Размер фондов, которые могут быть получены каждым отдельным предпри­ятием путем переговоров с плановыми органами, ограничен сверху и снизу.

Планы выполняются путем инвестиционной деятельности. Определенный размер ин­вестиций создает определенный объем готовой продукции, которая затем сдается госу­дарству. Государство (плановые органы) не знает в точности и не может проконтролиро­вать в точности объем инвестиционной деятельности.

График производственной функции (отношение между инвестициями и выпуском продукции) имеет ^образную форму и лежит ниже плановой прямой по крайней мере для одного из возможных объемов получаемых фондов (а возможно, и для множества таких объемов).

На рис. 5.8 изображена ситуация, когда плановая экономика работает эффективно (опираясь на полицейский плановый режим). Плановые органы устанавливают план, ко­торый может быть выполнен предприятиями только при полном использовании всех вы­деляемых фондов. Для теневой деятельности не остается ничего. Частные доходы эконо­ мических агентов (директоров предприятий и их сообщников по теневому бизнесу) равны нулю. Постоянный пересмотр производственных планов и норм выработки приводит к тому, что система постоянно находится в точке равновесия с максимальным использова­ нием имеющихся ресурсов.

Явлинский считает, что такое равновесие возможно только при очень быстром экс­ тенсивном экономическом росте. Равновесие А на рис. 5.8 уникально в том смысле, что оно находится как раз на точке перегиба, там, где возрастающая отдача от масштаба сме­ няется убывающей. Попытайтесь провести прямую линию из начала координат, которая пересекала бы график производственной функции в любой точке правее точки А, и вы убедитесь, что в этом случае под графиком будет целая область, в которой предприятие выполняет план. Иначе говоря, в экономике должен постоянно идти процесс создания новых предприятий (расширения, а не углубления сферы хозяйственной деятельности), с тем чтобы все они эксплуатировались в той области (до точки А или в крайнем случае в этой точке), где нет еще убывающей отдачи от увеличения масштаба.

Начальная стадия смягчения планового режима. По мере того как советская эконо­ мика развивалась и увеличивалась в размерах, возможности для такого экстенсивного роста становились все уже. Общего объема имеющихся в стране ресурсов стало не хватать для создания все новых производств. Поэтому объем выделяемых каждому предприятию ресурсов должен был сдвинут правее точки А на рис. 5.8. Это и произошло после смерти Сталина. Смена жесткого сталинского планового режима более мягким была предопреде­ лена объективной логикой экономического роста.

Последствием этого стало появление на древе планового хозяйства такой червоточи­ ны, которая через 35 лет привела его к гибели. Что же произошло? Посмотрим сначала на рис. 5.9.

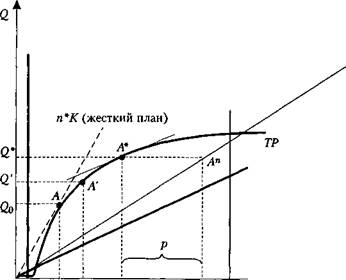
Рис . 5.9. Начальная стадия смягчения планового режима

Верхняя граница выделяемых фондов (и реальный размер фондирования) сдвигается вправо, правее точки перегиба графика производственной функции. При этом сохранение прежнего жесткого планового режима уже невозможно в силу убывающей отдачи, старые нормы действительно не могут соблюдаться (не случайно общее снижение ресурсоотдачи было главной проблемой экономики развитого социализма).

Плановые нормы смягчаются. Это не принципиальное устранение плановой экономи­ки, а именно лишь смягчение норм. На рис. 5.9 это показано в форме новой прямой линии «смягченный план» (пхК)с наклоном меньшим, чем на рис. 5.8. Меньший наклон плано­вой линии как раз и означает смягчение норм — на тот же объем фондов устанавливается менее жесткое задание по выпуску или выделение дополнительных фондов сопровожда­ется (относительным) снижением планового задания.

При такой ситуации у предприятия впервые появляется свобода выбора: в самом деле, график производственной функции лежит выше плановой линии на целом сегменте, за­штрихованном на рис. 5.9. Максимизация ресурсов для теневой деятельности впервые вы­ходит из сферы потенциальной в сферу реально достижимого.

Нетрудно доказать, что решение этой задачи достигается в точке А * на рис. 5.9, там, где касательная к графику производственной функции имеет тот же наклон, что и плановая прямая. Выпуск продукции равен Q *, реальный объем затраченных ресурсов равен /*, но по плану на объем производства Q * можно получить фонды в размере К*. Разница между этими двумя величинами (малое р на рис. 5.9, которое есть не что иное, как максимизиру­емая величина) используется предприятием в его неподотчетной, левой, теневой деятель­ности.

Здесь очень важно, что для плановых органов (наблюдающих лишь отчетные величи­ны, т. е. точку А" на рис. 5.9) ситуация первоначально тоже выглядит благоприятнее, чем при прежнем, жестком плановом режиме. Ведь более жесткий план (и, в частности, ста­линский режим, возвращающий систему в точку А) приведет не к росту, а к снижению выпуска готовой продукции. Если государство стремится к максимизации выпуска, не обращая внимания на снижение эффективности (относительный рост затрат), то, однаж­ды попробовав смягчение планового режима, оно придет к выводу, что экономикой лучше управлять в условиях оттепели. И наша история показывает, что в начальный период от­тепели наблюдается действительно медовый месяц государства и его предприятий — рас­ширяются их права и самостоятельность, ведутся глубокомысленные дискуссии о роли экономических стимулов и т. д. Предприятия отвечают па это ростом инвестиций и вы­пуска продукции (в полном соответствии с нашей моделью). То, что при этом растет и черный рынок, вначале особенно не волнует и трактуется как отдельные искажения.

На самом деле под завесой хрущевских, косыгинских и затем горбачевских реформ идет коррозия системы, и эта коррозия с неизбежностью приводит правящие круги к попытке остановить реформы и повернуть их вспять (в сторону нового ужесточения режима плано­вого хозяйства). Обратимся к рис. 5.10, иллюстрирующему следующую стадию процесса.

Циклы «отпуска» и «завинчивания гаек» в плановой экономике. По мере смягчения планового режима растут не только инвестиции и выпуск готовой продукции, растет и расход ресурсов каждым отдельным предприятием, причем растет быстрее, чем выпуск продукции (это видно из того, что растет доля ресурсов, поступающих па черный рынок).

Наступает момент, когда даже ориентированный на вал затратный механизм плановой экономики не может полностью игнорировать снижение эффективности. Все мы еще пом­ним лозунги типа «экономика должна быть экономной». В терминах данной модели это оз­начает, что каждому отдельному предприятию задается более жесткий, чем ранее, ресурс­ный режим. Верхняя граница фондов начинает ощущаться предприятиями в их торговле с властями.

В этих условиях дальнейшее смягчение планового режима ведет не к росту инвести­ций и выпуска продукции, как ранее, а к их снижению. Черный рынок продолжает разрастаться еще более быстрыми темпами. На рис. 5.10 такому состоянию соответствует точ­ ка Л' с объемом инвестиций /', объемом выпуска Q ' и размером ресурсов на черном рынке р' = К Г. В ответ на снижение норм (еще меньший наклон плановой прямой п' х К на рис. 5.10) предприятия не могут увеличить объем привлекаемых фондов просто потому, что они и так выбирают их до верхней границы Q , задачу максимизации левых доходов решают просто — снижая инвестиции и выпуск ровно на ту величину, на которую им по­ зволяют сделать это новые, более мягкие нормы.

О К К = 1 Г 1* р' К* К К,1

Рис . 5.10. Циклы «отпуска» и «завинчивания гаек» в плановой экономике

Разумеется, данное обстоятельство долго не ускользает от внимания социалистиче­ ского государства. Естественной реакцией властей является попытка нового ужесточения планового режима. Экономика начинает развиваться циклами: «либерализацияужесто­ чение» и т. д.

Крах советской плановой экономики. Один из важных выводов, к которым приводит анализ данной модели, таков: если на начальной стадии либерализации планового режима и собственник (плановые органы), и агенты (госпредприятия) довольны результатами изменения режима (растет и плановое производство, и черный рынок), то на стадии «за­ винчивания гаек» интересы собственника и директора расходятся. Неудивительно по­ этому, что по мере повторения этих циклов система все более разбалтывается и выходит изпод контроля собственникагосударства. С каждым раундом такой борьбы права и самостоятельность предприятий становятся все шире и все труднее лишать их этих прав и «прижимать» теневую экономику. Последний аккорд — борьба с «нетрудовыми дохо­ дами» — прозвучал уже в годы «перестройки».

Непримиримое уже противоречие между собственникомгосударством и директорами вкупе с новыми предпринимателями и деятелями теневой экономики переросло в настоя­щий системный кризис, и в короткой схватке в августе 1991 г. директора вышли оконча­ тельными победителями в борьбе против бывшего собственника.

Вдвоем одни
Одни вдвоем
Вдвоем как втроем
Под па па па
Под паль мой
Под пальмой мы живем. (19261927)

Т. С. Элиот (18881965)

В параграфе 5.3.2 мы рассмотрели понятие производственной функции с двумя переменными К и L (или производственной функции в длительном периоде) — изокванты. Вернемся вновь к этой проблеме и изобразим множество изоквант фирмы (рис. 5.11). Семейство изоквант (карта изоквант) базируется на предпо­ ложении, что производственный выбор фирмы состоит из большого (практиче­ ски неограниченного) количества альтернативных процессов. Каждой изокванте соответствует определенный объем выпуска, и величина объема увеличивается по мере того, как фирма перемещается к более высокой изокванте. На каждой изокванте факторы производства К и L можно заменять друг на друга, при этом объем выпуска остается величиной постоянной. Предельная норма технического замещения ( MRTS ) определяет наклон изокванты. Как и кривые безразличия по­ требителей, изокванты являются выпуклыми линиями. В двухфакторной модели выпуклость изокванты вызвана действием закона убывающей предельной нор­ мы технического замещения.

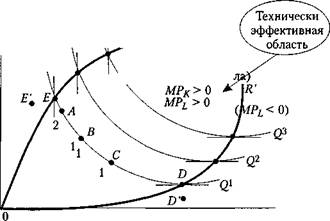К

Рис . 5.11. Изокванты , MRTS и «пограничные линии»

Закон убывающей предельной нормы технического замещения : по мере того как один фактор производства замещается на другой , процесс замещения стано­вится все более трудным : для поддержания данного объема производства требует­ся все более возрастающий объем замещающего фактора .

Так, перемещение от точки А к точке В предполагает, что одна единица труда за­меняет собой две единицы капитала, движение же от точки В к точке С подразу­мевает, что одна единица труда заменяет собой уже только одну единицу капита­ла и т. д.

Этот закон аналогичен закону убывающей отдачи, но учитывает изменение не одного, а двух факторов производства.

В точке D на изокванте Q t величина MRTS = 0. Это означает, что дальнейшее увеличение труда не способно заменить собой капитал без уменьшения объема про­изводства. В данной точке ( D ) предельный продукт труда равен нулю ( MP L = 0). Если увеличить объем труда сверх этого, не изменяя объем капитала, то переме­щение от точки D к точке D ' приведет к снижению объема выпуска: точка D ' нахо­дится на стадии III производственной функции для труда и на стадии I — для капитала (здесь капитал недоиспользуется, а труд избыточен).

В другом экстремуме (точка Е) изокванта вертикальна, и по тем же причинам предельный продукт капитала является величиной отрицательной; Е' находится на стадии III для капитала, и на стадии I — для труда (здесь труд недоиспользует­ся, а капитал избыточен). Линии ( OR и OR '), отделяющие технически эффектив­ную область от технически неэффективных, называются «пограничными линия­ми» ( ridge lines ).

По аналогии с предельной нормой замещения ( MRS ), норма технического за­мещения одного ресурса другим равна соотношению предельных продуктов этих ресурсов:

dL MP K (5.13)

Ах, роботы, ах, роботы, Спасибо вам за хлопоты, Вы наши избавители От тяжкого труда. Остался нам, родителям, Удел неутомительный: Любовь, деторождение, Куренье и еда.

В. В. Посувалюк (19401999)

Важность заменяемости факторов производства объясняется их относительной редкостью. При уменьшении доступности предложения факторов объем производ­ства фирмы зависит от ее способности осуществлять замену ресурсов. Степень за­меняемости одного фактора на другой измеряется сопоставлением изменения ве­личины MRTS с изменением соотношения ( K / L ). При этом возможны два крайних случая.

В первом крайнем случае ресурсы являются совершенными субститутами, и изокванты приобретают вид прямых линий: MRTS (наклон изокванты) постоя­нен при изменении К/ L (рис. 5.3, а).

Во втором крайнем случае факторы производства являются совершенными комплементами без возможности замены, а изокванты приобретают L образную форму (рис. 5.3, б).

Форма линий изоквант зависит от степени заменяемости одного фактора про­изводства на другой. Степень заменяемости измеряется эластичностью замены (а), которая определяется как изменение величины K / L , поделенное на соответ­ ствующее изменение величины MRTS :

A ( K / L ) d ( K / L ) MRTS

а = —— —— или о = 7— — . ( К \ л \

A(MRTS) dMRTS K/L ^.14)

Эластичность замены всегда является положительной величиной, которая из­ меняется между нулем и бесконечностью. Например, если два фактора производ­ ства совершенно заменяемы, то MRTS является величиной постоянной, d ( MRTS ) = = 0, а величина а бесконечно велика. В случае совершенных комплементов вели­ чина К/ L постоянна; d ( K / L ) = 0, а а = 0.

Таким образом, чем больше величина а, тем технологически проще один фактор производства заменить на другой. В табл. 5.4 приводятся примеры эластичности заме­ ны на основе исследования американской и японской экономики периода 1950х гг.

Таблица 5.4
Эластичность замены труд капитал отдельных отраслей

Источник : Arrow K.J. et al. Capitallabor substitution and economic efficiency //Review of Economics and statistics. Aug . 1961. P . 240.

Самая низкая эластичность замены присуща швейной промышленности, где машины являются слабыми субститутами человеческого труда. Напротив, самые высокие показатели а на транспорте, добыче нефти и газа, где высока степень заменяемости труда и капитала.

5.8. Эффективная комбинация двух переменных факторов

Два небольших идиотизма круглой формы Обменивались мнениями. Свободными. Свободно.
И мненья их во многом совпадали.
Ну не чудно ль?! (2000)

Валерий Гвоздей

Комбинация факторов производства, которую выбирает фирма, зависит от относительных издержек. Структура издержек считается эффективной, если при их данном уровне достигается максимум объема выпуска или издержки мини­мальны при данном объеме выпуска. Издержки (С) равны сумме использован­ных факторов производства (в денежных единицах):

C = wL + rK , (5.15)

где w — ставка заработной платы (цена единицы труда);

г— процент на капитал (иногда величину г называют рентной ценой единицы капитала).

Уравнение издержек в теории производства аналогично бюджетному ограниче­нию в теории потребления. Уравнение издержек или уравнение бюджетного огра­ничения производителя формирует изокосту. 1

Изокоста — линия , все точки которой представляют одинаковые по ценности соче­тания разных количеств двух факторов производства .

Из равенства 5.15 можно получить уравнение изокосты для капитала и для

труда:

„ С w T

К = 1, (5.16)

г г

где w / r — наклон изокосты относительно оси фактора труда;

1 = к, (5.17)

WW

где r / w — наклон изокосты относительно оси фактора капитала.

Umweg ist der landste Weg , Самый долгий путь — окольный,

Abweg ist der schwerste Weg , самый тяжкий — ложный; больно

Wer em treues Herz verlor , за глупца, что выбирает

1st der allergro (3 te Tor . путь, где друга потеряет.

Ernst Wiechert (18881960) Перевод С. X . Симкина

х о о ? «изос» («равный» — греч.); consto («стоить» — лаг.).

Оптимальный объем производства находится на основании известного прин­ципа: минимальные затраты при данном выпуске или максимальный выпуск при данных затратах. Графически оптимальный объем производства с двумя переменны­ми ресурсами определяется наложением карты изокост на изокванту (рис. 5.12, а) либо карту изоквант на изокосту (рис. 5.12, б).

При наложении карты изоквант на карту изокост можно получить линию роста фирмы ( expansionpath ) или изоклиналь. 1

Линия роста фирмы ( изоклиналь ): линия , определяющая совокупность оптималь­ных объемов производства фирмы как множество касаний карты изокост и изоквант . Изоклиналь показывает оптимальные объемы производства фирмы при разных про­изводственных мощностях .

Рис . 5.12. Определение оптимального объема производства методом : а ) минимальных затрат при данном объеме производства ; б ) максимального производства при данных затратах

Так как наклоны изоквант и изокост равны в точках касания, изоклиналь со­стоит из комбинаций, уравновешивающих MRTS и отношение затрат:

MRTS ар/г. (5.18)

Изображение изоклинали дано на рис. 5.13.

То, что представляется изменением вокруг нас, — лишь скорость судна, покидающего этот мир.
Джалал ad дин Руми (12071273)

Зависимость прироста выпуска продукции от увеличения всех производствен­ных факторов является одной из важных характеристик производственного процесса фирмы в долгосрочном периоде. При рассмотрении производственной функ­ ции часто исходят из того, что при увеличении объема применяемых факторов про­ изводства пропорционально возрастает и объем производства. Однако на практике это бывает далеко не всегда.

Рис . 5.13. Линия роста фирмы ( изоклиналь )

Часто (но не обязательно всегда) при увеличении масштабов относительно мелкого производства выпуск растет опережающими темпами по сравнению с увеличением факторов производства. В таком случае говорят, что имеет место возрастающая отдача от масштаба.

Затем, по мере дальнейшего роста объемов производства, отдача от масштаба может равняться приросту факторов производства. Это случай постоянной отда­ чи от масштаба.

Наконец, достигнув какогото уровня, отдача от масштаба замедляется по сравнению с увеличением объемов применяемых факторов производства. Это — убывающая отдача от масштаба.

Для оценки отдачи от масштаба используют понятие однородности. Произ­ водственная функция называется однородной, если при увеличении всех факто­ ров производства в k раз объем выпуска увеличивается в k раз. Здесь t — показатель степени однородности. Таким образом, производственная функция Q = Q ( L , К) является однородной в степени t , если:

* Q Q ( kL , kK ). (5.19)

Если t = 1, то функция однородна в первой степени, а производство демонст­ рирует постоянную отдачу от масштаба. В этом случае говорят, что производ­ ственная функция линейнооднородная.

Если t > 1, то имеет место возрастающая отдача от масштаба.

Если t < 1 — налицо убывающая отдача от масштаба.

Поясним понятие отдачи от масштаба с помощью графика (рис. 5.14).

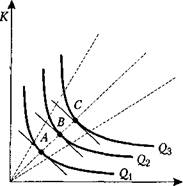
Когда производственный процесс фирмы характеризуется возрастающей от­ дачей от масштаба (отрезок ОА луча), изокванты становятся ближе друг к другу. Это означает, что при пропорциональном увеличении труда (5, 10, 15 и т.д.) и капитала (1, 2,3 и т. д.) объем производства возрастает ускоряющимися темпами.

О L

Рис. 5.14. Отдача от масштаба

При убывающей отдачи от масштаба (отрезок АВ луча), напротив, изокванты располагаются все дальше друг от друга, так как требуется все большее и большее количество факторов производства для увеличения объемов производства.

О L

Рис . 5.15. Изокванты однородной производственной функции

При постоянной отдаче от масштаба (рис. 5.15) изокванты располагаются рав­ номерно.

Отдача от масштаба существенно различается для разных фирм и отраслей. При прочих равных условиях, чем больше отдача от масштаба, тем более крупные фир­ мы действуют в данной отрасли. Обычно производственные отрасли характеризу­ ются большей отдачей от масштаба, чем сферы услуг, так как в материальном про­ изводстве требуются существенные капиталовложения в оборудование.

Вернемся к производственной функции КоббаДугласа ( Q = Л? а А*). Ее сте­ пень однородности равна (а + Ь). Особым случаем является функция Q = D /2 K [/2 , когда однородность функции КоббаДугласа линейна, т. е. демонстрирует посто­ янную отдачу от масштаба.

Однородная производственная функция обладает следующими свойствами. Вопервых, отношение предельных продуктов ( MP K / MP L = MRTS ) не меняется, если затраты (К и L ) изменяются пропорционально. Это значит, что в каждой точ­ке любого луча, исходящего из начала координат на рис. 5.15 (т. е. в точках А, В, С и т. д.), наклон изоквант ( Q ,, Q r Q 3 и т. д.) постоянен.

Вовторых, в соответствии с теоремой Эйлера сумма частичных производных относительно независимой переменной равна произведению зависимой перемен­ ной на степень однородности.

Теорема Эйлера : если выражение Y = ( X v Х 2 , ¦¦, Х п ) однородно , то ^^ ЭУ / Э ^, = tY , где t — показатель степени однородности .

В случае двухфакторной модели это означает, что:

tQ Lx MP L + KxMP K . (5.20)

Эти два свойства однородной производственной функции особенно важны при анализе издержек (см. главу 6), а также при изучении распределения дохода в конкурентной экономике.

Эластичность выпуска и отдача от масштаба. Если считать формой произ­ водственной функции длительного периода степенную функцию:

Q = AL a Kb при а + Ъ = 1, то

показатели а и Ь равны коэффициентам эластичности по факторам:

1

_ MP L _ aAK ^ L "' _ bQl ~ AP L ~ ARtLT 1 ~°" _ MP K РЛГХ М

AP K AL a K ^

Для характеристики отдачи от масштаба используется коэффициент эластич­ ности выпуска от масштаба (е„ к ). Данная величина показывает, на сколько из­менится выпуск, если темп роста объемов использования обоих факторов увели­ чится на единицу:

dQ К
^¦" = dK Q (5.21)

Коэффициент эластичности выпуска от масштаба характеризует степень од­ нородности производственной функции, т. е. отдача от масштаба может быть представлена в универсальной форме:

Q , Ke & Q ( tL , tK ). (5.22)

Если показатель степени (е„ ? ):

• >1, то отдача от масштаба возрастает;
• = 1, то отдача от масштаба постоянна;
• <1 то отдача от масштаба снижается.

Теорема ВикселяДжонса: эластичность выпуска от масштаба равна сумме эластичностей выпуска от используемых факторов:

е ш = е <ц. + е ак ( 5 23 )

Доказательство. Полный дифференциал однородной функции Q = f ( L , K ) равен:

DQj i dL + d i dK < 5 24 >

При пропорциональном изменении факторов имеет место:

dt dL dK , dt , , dt ,.,..

Т = Т = Т =»Л = Т Я,Л Т Х. (5.25)

Подставив 5.25 в 5.24, получим:

Умножим обе части полученного равенства на t / Q x dt . dQ t _ = df _ L _ df _ K _ dt ' Q ~ dL Q + dK ' Q '

а это есть не что иное, как выражение 5.23, что и требовалось доказать.

Мы два различных бытия. Мы зеркала — и ты, и я. Я все возьму и углублю,
Но отражая, — преломлю. (февраль 1913)

Зинаида Николаевна Гиппиус (18691945)

В главе 4 рассматривалась теория потребления, объясняющая природу линии спроса. Глава 5 посвящена теории производства, объясняющей природу линии предложения. Данные две теории являются симметричными — модели, рассмат­ риваемые в них, различаются лишь символами (табл. 5.5).

Таблица 5.5
Симметричность теорий потребления и производства

/ Р х Х+ P Y Y

7. Оптимальный набор товаров:

ми х

Х , У

у ±у

8. Линия доходпотребление (РРС) 9. Кривая спроса ( Q D )

Уравнение пзокосты:

C = wL + rK

Оптимальная комбинация ресурсов:

MP , w MRTS LK =

L _

МР К г

Линия роста (изоклиналь)

Кривая предложения (Q 5 )

Существенное различие между этими теориями заключается в следующем. Теория производства статистически определена, все взаимозависимости между факторами этой теоретической системы практически измеримы и технологиче­ски определяемы. Напротив, теория потребительского поведения оперирует ин­дивидуальными вкусами и предпочтениями, которые затруднительно измерять практически.

Данными 9 парами потребления и производства симметричность двух теорий отнюдь не исчерпывается. Существует множество иных парных категорий, кото­рые не рассматриваются в данном курсе.

1. Почему в краткосрочном периоде предельный продукт труда сначала растет, а по­ том снижается?
2. Почему фирма, решающая, привлекать ли ей дополнительные факторы производ­ ства, должна больше учитывать предельные, а не средние продукты?
3. Что такое производственная функция? Почему результатов анализа, полученных на основании производственной функции, недостаточно для принятия решений о деятельности фирмы?
4. Когда известный правительственный деятель переезжал из Москвы в Петербург, показатель среднего уровня умственного развития в обоих городах поднимался. Объясните смысл этой шутки, сопоставив средний и предельный продукт.
5. Чем отличаются производственные функции в краткосрочном и долгосрочном пе­ риодах?
6. Что такое предельная норма технического замещения ресурса и какое практиче­ ское значение она имеет для деятельности фирмы?
7. Если бы не существовал закон убывания предельного продукта, то весь объем ми­ рового предложения продуктов питания можно было бы вырастить в одном цве­ точном горшке! Согласны?
8. Почему оптимум производителя достигается в точке касания изокванты и изокос ты?
9. Почему линии изоквант имеют разные формы? Может ли изокваната по аналогии с кривой безразличия быть вогнутой к началу координат?
10. Может ли фирма иметь производственную функцию, характеризующуюся сначала возрастающей, затем постоянной отдачей от масштаба и, наконец, убывающей по мере увеличения выпуска?
11. Может ли процесс производства характеризоваться одновременно убыванием пре­дельного продукта фактора и возрастающей отдачей от масштаба?
12. Вашему вниманию предлагается «Баллада о директоре завода», написанная в 1983 г. Юрием Ключниковым.
    Сибирский город, а какой — неважно.

Важнее то, что в нем варили сталь,

Идущую на танковые башни

Для Т34, и представь,

Не то, что эта сталь огнем хлестала

Чужих солдат и берегла своих,

А то, что этой стали было мало

И что однажды телефон звонит.

Алло, директор? Да.

Товарищ Сталин Вас вызывает.

Сталин? Я всегда...

И голос глуховатый в трубке:

— Стали

Даете мало. Слышите?

— Да, да!

Я слышу, мы, конечно, примем меры, —

Директор зачастил, —

Но горняки...

Не сразу вник он, от волненья серый,

Что слушает короткие гудки.

Но справился с волненьем, вызвал замов,

Потребовал повысить домен мощь.

А через месяц срочной телеграммой

Был вызван в Кремль.

... Москва. Глухая ночь

Дубовый тамбур. Молотов. Устинов,

Калинин и другие. Холод стен. И сквозь усы знакомые, густые Негромкие слова:

— Товарищ Эн

Был нами извещен, что сталь сегодня Решает все. И плохо понял нас. Он выпуск лишь на семь процентов поднял. По существу не выполнил приказ. Страна в крови. Такой работы линия Преступна. Предлагаю расстрелять. Кто — «за?» Что, у товарища Калинина 'Есть возраженье?

— Трудно поправлять, —
Калинин встал, — подобную работу.
Но может быть, последний срок дадим?
... Вошел директор в Спасские ворота
Черноволосым,

А ушел седым.

Он дома, возвратившись из столицы,

Собрал актив па несколько минут.

— Мы будем спать, обедать и трудиться
В цехах завода. Все, нас домны ждут.
Металл пошел, пошел он вдвое, втрое...
Ну а потом Тацинская была*,

Огонь и гром морозовского боя И Прохоровки дымные дела.

Проанализируйте данный текст. Постройте примерную модель производственной функции сталелитейного предприятия «до звонка из Кремля». Приростом каких факто­ров производства можно объяснить увеличение выпуска на семь процентов «после звон­ка»? Каким образом было возможно увеличить объем выпуска в «дватри раза» после «вызова в Кремль»? Поясните это с помощью линии производственной функции.

Задача

13. Производственная функция фирмы «Емельян Пугачев» имеет вид:

Q = ЮК 0 ' 5 ! 05 . Производственная функция фирмы «Урюпинск» имеет вид:

Если обе компании используют одинаковые количества труда и капитала, у какой из них объем выпуска будет больше? Ответ: одинаковый выпуск.